Learning Congestion in Multi-Agent Path Finding

September 10, 2024

By Jake Gonzales

Overview: This blog post explores the integration of deep learning techniques to predict congestion in Multi-Agent Path Finding, potentially leading to increased scalability and efficiency in complex, dynamic environments.

Introduction

Multi-agent path finding (MAPF) is a fundamental problem in artificial intelligence and robotics, involving the coordination of multiple agents to navigate from their respective origins to destinations without collisions. At its core, MAPF can be formulated as a constraint satisfaction problem, where the primary objective is to determine collision-free paths for all agents while optimizing various criteria such as path length, system throughput, and completion time. The problem's complexity stems from the need to consider the interdependencies between agents' movements and the exponential growth of the solution space as the number of agents increases.

The most significant challenge in MAPF is scalability, as the computational complexity grows rapidly with the number of agents and the size of the environment. Current state-of-the-art approaches to tackle this challenge include Conflict-Based Search (CBS), a two-level algorithm that separates path planning and conflict resolution. CBS operates by initially computing optimal paths for each agent independently, then identifying and resolving conflicts through a constraint tree search. This method allows for efficient handling of larger instances by focusing computational resources on resolving conflicts rather than exhaustively exploring the joint state space of all agents.

Congestion is undoubtedly a critical factor in MAPF scenarios, particularly in high-density environments or those with limited resources. Predicting and managing congestion across the flow of agents is crucial for improving overall system throughput and anticipating agent interactions. By incorporating congestion prediction into MAPF algorithms, we can potentially enhance path planning strategies, leading to more efficient and robust solutions in complex, multi-agent environments.

Congestion Prediction

Background and Setup

In recent years, machine learning methods have gained significant traction in the field of Multi-Agent Path Finding (MAPF), offering promising avenues to enhance the scalability and efficiency of existing solvers. These data-driven approaches leverage patterns and heuristics learned from vast amounts of MAPF instances to guide search algorithms, prune search spaces, or directly approximate solutions. By incorporating ML techniques, researchers aim to overcome the computational bottlenecks associated with traditional exact solvers, especially when dealing with large-scale problems involving hundreds or thousands of agents. In light of this, we developed a deep learning approach to perform congestion prediction across warehouse floors in MAPF scenarios. This method aims to anticipate areas of high agent density and potential conflicts, thereby informing path planning decisions and improving overall system throughput.

Formally, we model the MAPF problem on a graph abstraction \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\), where \(\mathcal{V}\) represents the set of vertices (locations) and \(\mathcal{E}\) denotes the set of edges (connections between adjacent locations). Let \(A = \{a_1, a_2, \ldots, a_n\}\) be the set of \(n\) agents. Each agent \(a_i\) has a start vertex \(s_i \in \mathcal{V}\) and a goal vertex \(g_i \in \mathcal{V}\). Space and time is discretized, and at each time step, an agent can either move to an adjacent vertex or wait at its current vertex. A solution to the MAPF problem is a set of paths \(P = \{p_1, p_2, \ldots, p_n\}\), where \(p_i = \langle v_i^0, v_i^1, \ldots, v_i^k \rangle\) represents the path of agent \(a_i\), with \(v_i^0 = s_i\) and \(v_i^k = g_i\). The solution must satisfy the following constraints:

1. Vertex collision: \(\forall i \neq j, \forall t, v_i^t \neq v_j^t\)
2. Edge collision: \(\forall i \neq j, \forall t, (v_i^t, v_i^{t+1}) \neq (v_j^{t+1}, v_j^t)\)

The objective is typically to minimize a cost function, such as the sum of individual path lengths or the makespan (maximum individual path length). The computational complexity of optimal MAPF is NP-hard, necessitating the development of efficient approximate or bounded suboptimal algorithms for practical applications.

In our large hierarchical framework, we decompose the warehouse into subregions to better learn congestion patterns. We focus on learning congestion within these subregions, specifically utilizing a 14x14 subregion with obstacles. The number of agents in each subregion is determined by a heuristic based on the subregion size, resulting in 4-16 agents per subregion. Each agent's source-destination pair is set such that the agent starts on a boundary node of the subregion and attempts to reach the opposite boundary.

We connect these learned congestion models to nonatomic routing games to solve for equilibrium solution concepts of the traffic flow from large fleets of agents. This will be explained in a later blog post. In this context, each edge has an associated congestion function where we aim to learn this function across the map. The congestion function is expressed as:

where \(l(x)\) is the congestion function we are learning, \(A\) is the congestion coefficient matrix, \(x\) represents the flow (agents traveling across nodes), and \(b\) is the free flow time.

Data Preparation

We collected and prepared data from multiple instances of Conflict-Based Search (CBS). Our dataset comprises approximately 25,000 problem instances for training and 5,000 problem instances for testing. This extensive dataset allows us to capture a wide range of congestion scenarios and agent interactions within the defined subregions, providing a robust foundation to learn congestion.

Architecture

Our congestion prediction model is designed to capture complex spatiotemporal interactions while maintaining computational efficiency. The architecture integrates graph convolutional networks (GCNs), sequential processing, and attention mechanisms to model evolving agent interactions during planning.

We use GCN layers to encode spatial relationships within the environment. These layers enable the model to learn hierarchical representations of the graph structure, capturing both local and global topological features. GCNs, however, lack in capturing long-range dependencies, which motivates the use of a mutli-head attention mechanism. This component allows for dynamic, learned weighting of different time steps and spatial locations, effectively creating flexible areas of focus across at different timesteps and spatial locations.

To address the temporal aspect of congestion, which is crucial in MAPF scenarios, we employ a gated recurrent unit (GRU). This recurrent component processes the sequence of graph embeddings, enabling the model to capture and retain information about the temporal evolution of congestion patterns. The GRU's ability to model long-term dependencies is particularly valuable in scenarios where past agent movements significantly influence future congestion states.

Our architecture's design principles emphasize the balance between expressive power and computational efficiency. By integrating GCNs for spatial modeling, recurrent processing for temporal dynamics, and attention mechanisms for adaptive feature selection, we create a model capable of capturing the complex, interrelated nature of congestion in MAPF scenarios. This approach enables our model to provide context-aware congestion predictions that can be efficiently updated in real-time, making it well-suited for integration into dynamic path planning algorithms.

Results

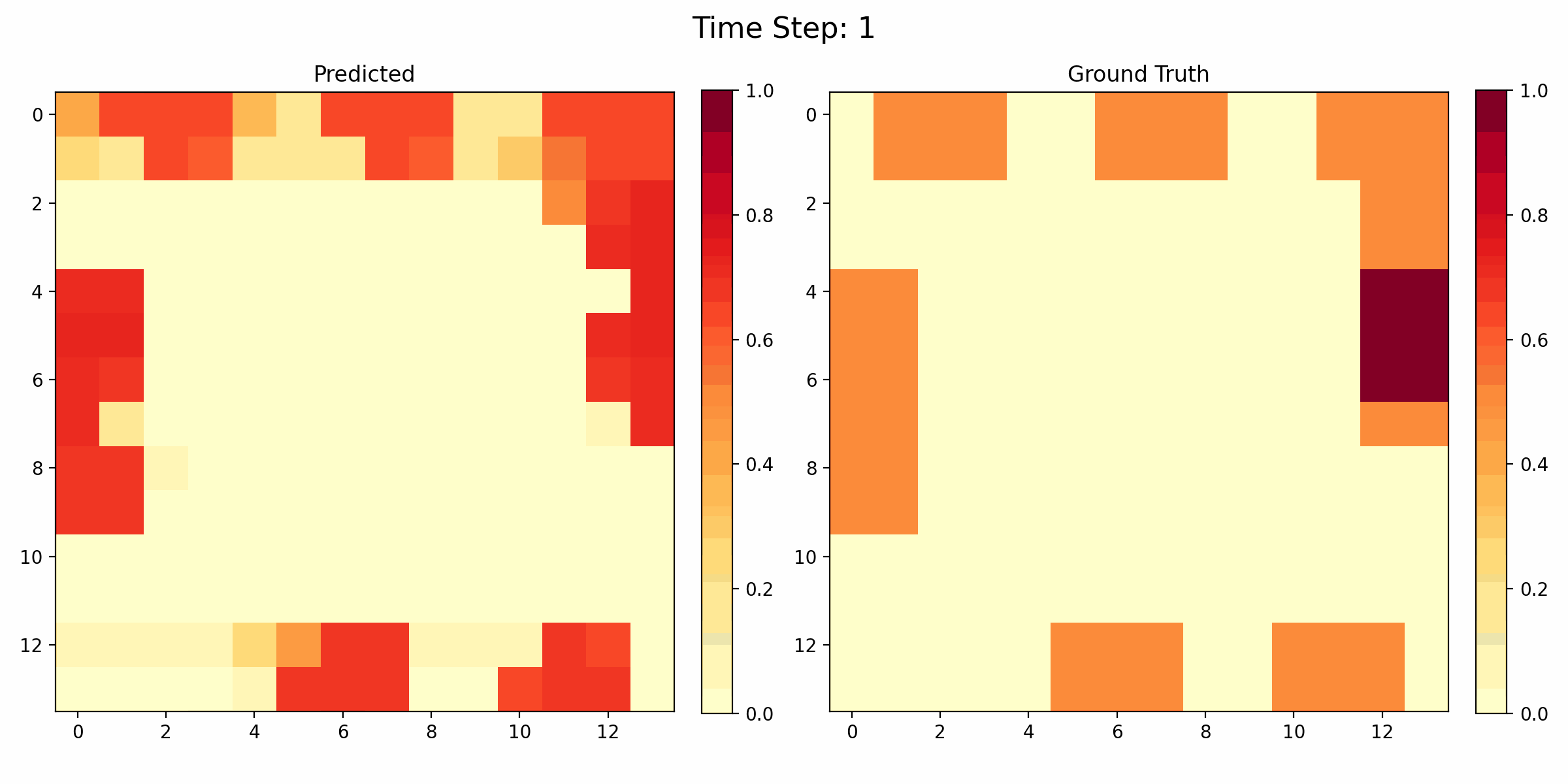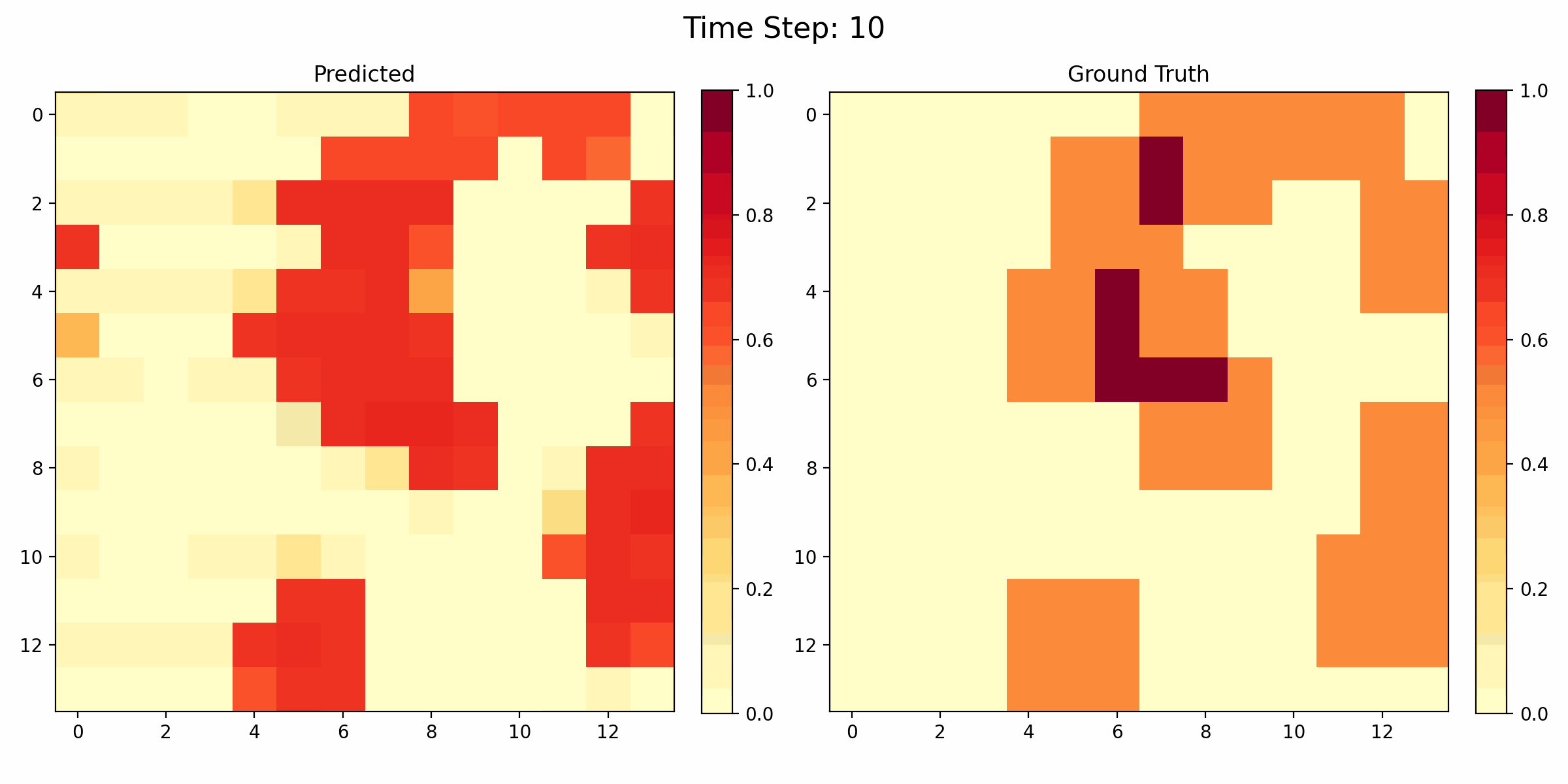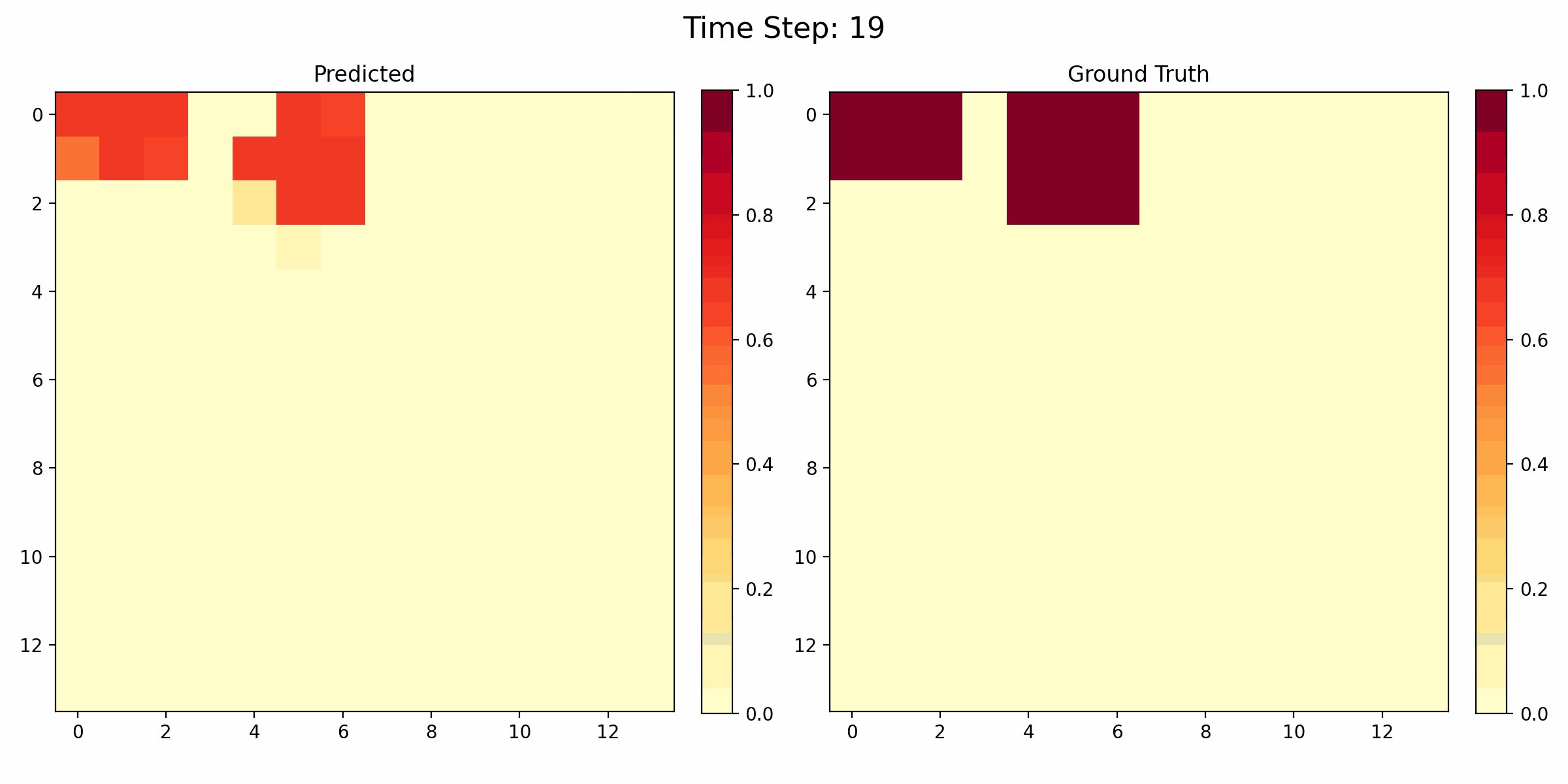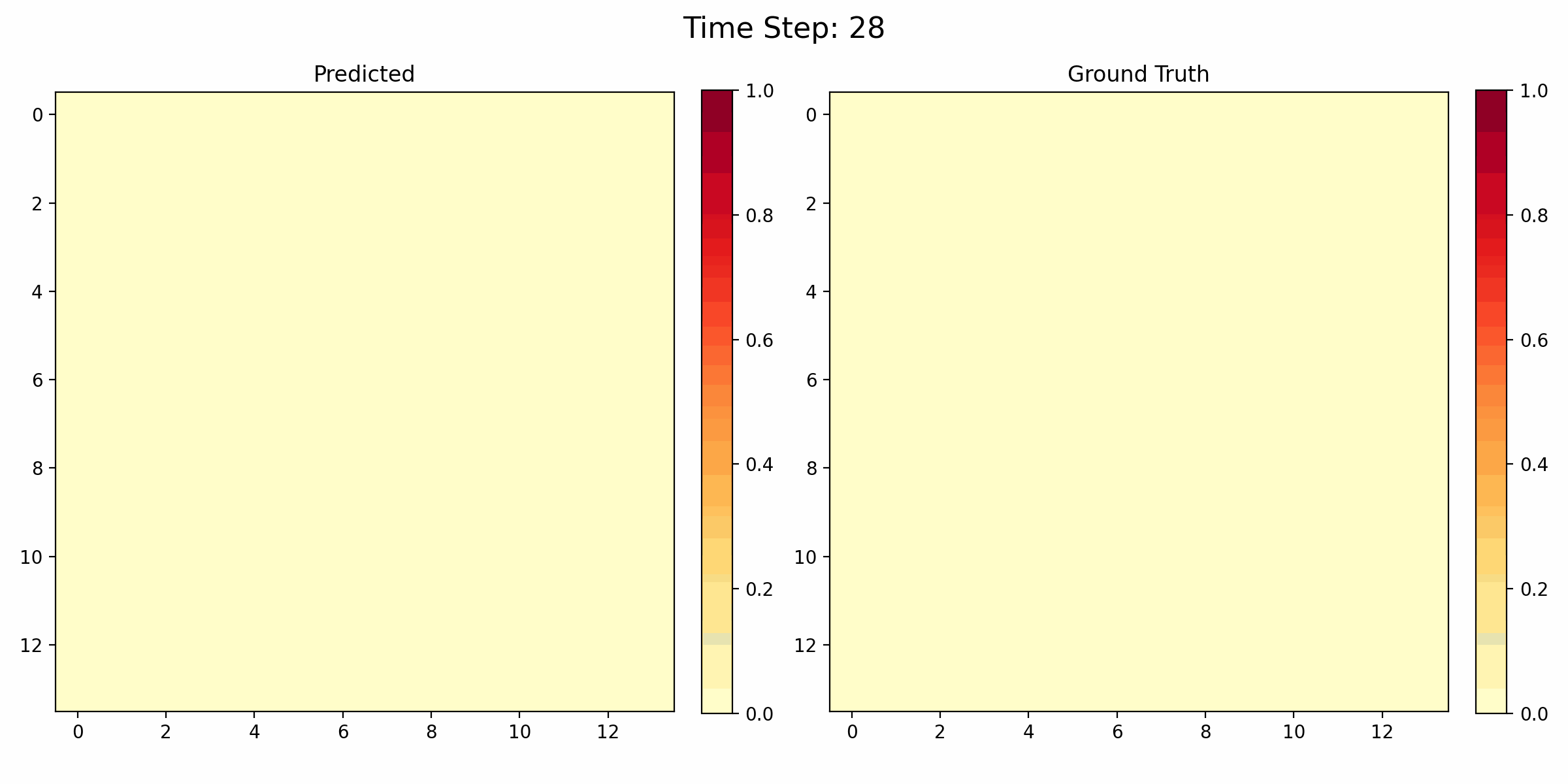
Temporal Congestion Prediction Visualization

The GIF above demonstrates an instance of prediction on a MAPF problem, showcasing the capabilities of our congestion prediction model. In the animation, we can observe the dynamic nature of congestion as agents navigate through the environment.

These results demonstrate the effectiveness of our deep learning approach in capturing both spatial and temporal aspects of congestion in MAPF problems. By accurately predicting congestion patterns, we can potentially improve path planning algorithms, leading to more efficient navigation and reduced conflicts in multi-agent systems.

Conclusion

In this blog post, we explored the integration of deep learning techniques to predict congestion in Multi-Agent Path Finding (MAPF) scenarios. This research opens up exciting possibilities for enhancing MAPF algorithms and their applications in various domains, including warehouse automation, traffic management, and robotics. By accurately predicting congestion patterns, we can develop more robust and efficient solutions for coordinating large numbers of agents in complex environments. This work pushes towards greater inclusion of deep learning in traditional MAPF approaches, potentially leading to breakthroughs in scalability and performance for multi-agent systems.

Note: The code for this project will be made available soon. Stay tuned for updates on how to access and implement these congestion prediction models in your own MAPF applications.